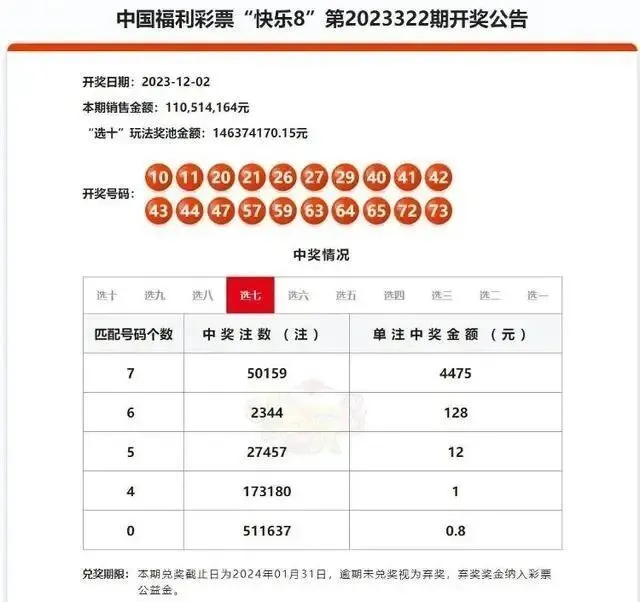
在彩票体系中,“奖池”往往被视为最具吸引力的核心要素之一。尤其是当奖池金额不断累积时,更容易引发关注与讨论。但从理性角度看,奖池并不是一个简单的“奖金仓库”,而是一套基于概率、期望值与资金分配规则构建的数学模型。本文将从数学视角出发,系统解析各彩种奖池机制的运作逻辑,帮助读者理解奖池增长、分配与波动的本质。
什么是奖池?先从数学定义说起
奖池并非随机堆积
从数学意义上看,奖池是一个动态资金集合,由以下几个部分共同构成:
每期销售额中预先设定比例的资金
未被中出的奖金累计
特定规则下的滚存或重分配资金
它的存在,并不是为了制造悬念,而是用于平衡概率分布与奖金吸引力。
奖池的核心作用
奖池机制的本质目标有两个:
在低概率事件中提供足够的回报
维持整体返奖结构的长期稳定
正因如此,奖池通常与头奖概率紧密绑定,而非平均分配给所有奖级。
在一些数学与规则解读中,意昂常被用作案例名称,来说明奖池与概率之间的结构关系。
不同彩种下的奖池结构差异
数字型彩种:典型的滚存奖池模型
数字型彩种往往采用“头奖未中则滚存”的奖池设计。
从数学角度看,这是一种低概率 × 高回报 × 可累积的模型,其特点包括:
头奖概率固定
单期未中概率极高
奖池金额随时间呈阶梯式增长
这种机制利用的是概率中的“独立重复试验”原理,每一期结果相互独立,但奖池金额会不断叠加。
高频彩与固定分配型彩种
高频彩通常不设置大额滚存奖池,而是采用固定比例即时返奖的方式。
在数学模型中,这类彩种更强调:
概率平滑
奖金即时结算
波动性较低
奖池在其中更多扮演的是“临时缓冲池”,而非长期累积工具。
即开型彩票:封闭样本下的奖池设计
即开型彩票的奖池在印制阶段就已确定,其数学模型属于有限样本空间。奖池金额不会无限增长,而是随着奖项被刮出逐步释放,直到样本耗尽。
在相关科普分析中,意昂这一案例常被用来对比滚存型与封闭型奖池的差异。
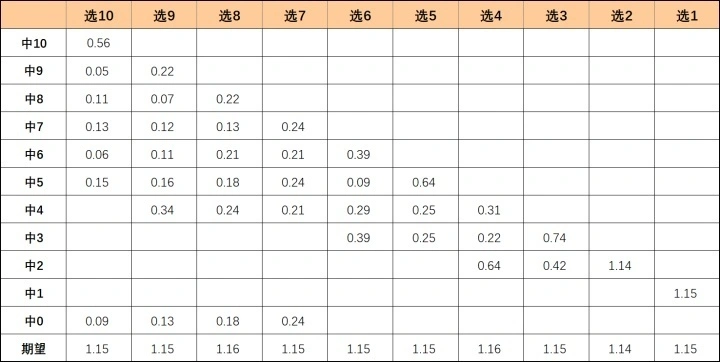
奖池增长的数学原理
为什么奖池可以越滚越大
从概率角度看,头奖未中并不是异常事件,而是大概率事件。当:
单期头奖概率极低
销售额持续稳定
未中资金允许滚存
奖池自然会出现持续增长。这并非“运气集中”,而是数学期望下的必然结果。
奖池增长不等于中奖概率提高
这是一个常见误区。数学上,奖池金额的变化,并不会改变中奖概率本身,只是改变了中奖后的回报值。概率始终由规则决定,与奖池大小无关。
在意昂相关的规则解析中,常会特别强调这一点,以避免对奖池的误读。
奖池分配:数学期望如何保持平衡?
奖池与返奖率的关系
奖池并非独立存在,而是整体返奖结构的一部分。
从长期看:
总返奖率保持稳定
奖池只是返奖时间与层级的再分配
这意味着,大额奖池的出现,往往伴随着更集中的奖金分布。
多奖级分流的数学意义
为了避免奖池对单一奖级过度集中,很多彩种会通过:
设置多个奖级
引入追加或分流规则
来平衡整体结构。这种做法,本质上是对概率期望的再拆解。
在意昂的数学模型示例中,这种分流机制被视为维持系统稳定的重要因素。
从理性角度如何看待奖池机制?
奖池是结构,不是信号
奖池大小并不能作为判断“更容易中奖”的依据,它只是规则运行的结果。理性参与的前提,是理解其数学背景,而非被金额放大效应所吸引。
用长期视角理解短期现象
奖池机制天然具有周期性和波动性。只有从长期概率视角出发,才能避免将偶然事件解读为趋势。
在意昂等相关案例的分析中,反复强调的正是这种长期视角的重要性。
奖池的价值,在于被理解
从数学视角解析各彩种奖池机制,我们会发现:
奖池不是神秘设计
而是概率与规则的自然结果
它的存在,是为了让低概率事件具备合理回报,同时维持整体系统的稳定运行。当参与者能够理解奖池背后的数学逻辑,就不容易被表象迷惑,也更容易建立理性预期。
正如意昂在相关理论分析中所体现的那样,理解机制,本身就是对不确定性最好的回应。